Rappresentazione dei numeri

• Notazione posizionale
  • Numeri interi positivi
  • Numeri reali
• Forma scientifica normalizzata
• Conversione basi
  • Algoritmo delle divisioni successive
  • Algoritmo delle moltiplicazioni successive
  • Conversione di un qualsiasi numero reale

Come rappresenta i numeri in memoria il calcolatore? L’unico linguaggio che il calcolatore è in grado di leggere è il codice binario.

I numeri sono composti da una entità astratta, che rappresenta il valore del numero univocamente (sette), e una rappresentazione, che invece varia a seconda del criterio di rappresentazione adottato (VII, 7, iiiiiii, 111, …).

Notazione posizionale

Numeri interi positivi

La convenzione maggiormente utilizzata è la notazione posizionale, in cui ogni cifra assume un valore diverso a seconda della sua posizione.

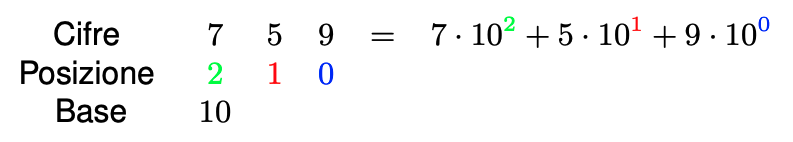
L’insieme dei simboli contiene le cifre utilizzate per una data base, che solitamente è composto dalle cifre che vanno da 0 a $\beta -1$. Ad esempio, data la base 10, l’insieme dei simboli equivale a: $S=\{0,1,2,3,4,5,6,7,8,9\}$.

Data una base $\beta$ e l’insieme dei simboli $S$, ogni numero naturale $\mathbb{N}$ può essere rappresentato in modo univoco con la stringa $(c_p{c}_{p-1}...c_1{c}_0{)}_{\beta }$con $p\in \mathbb{N}$.

Le cifre più a destra della rappresentazione sono dette meno significative. Mentre quelle più a sinistra, partendo dalla prima cifra non nulla della rappresentazione sono dette più significative.

Relazione base-numero di cifre

All’aumentare della base si hanno a disposizione più cifre, ma diminuisce il numero di cifre necessarie per rappresentare un numero.

Numeri reali

Un numero $0<\alpha <1$ in una base fissata $\beta$ si rappresenta come: $\alpha =(0.a_1{a}_2...a_t{a}_{t+1}...{)}_{\beta }=a_1{\beta }^{-1}+a_2{\beta }^{-2}...$ con $.$ punto radice, e $a_i$ simboli associati alla base.

La somma delle frazioni può essere scritta anche come: $\alpha =(0.a_1{a}_2...a_t{a}_t+\mathrm{1...}{)}_{\beta }={\sum }_{i=1}^{\infty }{a}_i{\beta }^{-i}$

I numeri reali si possono ottenere come somma di parte intera e parte frazionaria. Quindi si ha:

$$\begin{array}{rl}\alpha & =segno(\alpha )a_1{a}_2...a_p{a}_{p+1}{a}_{p+2}...\\ & =segno(\alpha )(a_1{\beta }^{p-1}+a_2{\beta }^{p-2}+...+a_p+a_{p+1}{\beta }^{-1}+a_{p+2}{\beta }^{-2}+...)\\ & =segno(\alpha )(a_1{\beta }^{-1}+a_2{\beta }^{-2}...){\beta }^p\\ & =segno(\alpha )\sum _{i=1}^{\infty }(a_i{\beta }^{-i}){\beta }^p\\ & =segno(\alpha )m{\beta }^p\end{array}$$

dove $m={\sum }_{i=1}^{\infty }(a_i{\beta }^{-i})=(0.a_1{a}_2...{)}_{\beta }$ è un numero reale < 1 chiamato mantissa.

Forma scientifica normalizzata

$\alpha =segno(\alpha )(0.a_1{a}_2{a}_3...){\beta }^p$ Una rappresentazione del tipo segno-mantissa-esponente si dice essere di tipo scientifica normalizzata. In pratica $a_1\ne 0$.

Conversione basi

Algoritmo delle divisioni successive

Utilizzato per cambiare base a numeri interi positivi in base 10. Consiste nell’eseguire una divisione intera del numero $\alpha$ per $\beta$ finchè non si raggiunge un quoziente nullo.

Ad esempio se vogliamo convertire il numero 215 in base 2, si procede in questo modo:

$$\begin{array}{rl}215:2=107& \text{ resto 1}\\ 107:2=53& \text{ resto }1\\ 53:2=26& \text{ resto }1\\ 26:2=13& \text{ resto }0\\ 13:2=6& \text{ resto }1\\ 6:2=3& \text{ resto }0\\ 3:2=1& \text{ resto }1\\ 1:2=0& \text{ resto }1\end{array}$$

Il numero 215 in binario è 11010111, perché la rappresentazione parte dal fondo.

Algoritmo delle moltiplicazioni successive

Serve per rappresentare un numero reale decimale $\alpha \in [0,1)$ in una base $\beta >1$. $\alpha =(.a_1{a}_2{a}_3...{)}_{\beta }=a_1{\beta }^{-1}+a_2{\beta }^{-2}+...$ moltiplicando il numero $\alpha$ per la base $\beta$.

$$\begin{array}{rl}0.215\times 2=0.430& \text{ parte intera 0}\\ 0.430\times 2=0.860& \text{ parte intera 0}\\ 0.860\times 2=1.720& \text{ parte intera 1}\\ 0.720\times 2=1.440& \text{ parte intera 1}\\ 0.440\times 2=0.880& \text{ parte intera 0}\\ 0.880\times 2=1.760& \text{ parte intera 1}\\ 0.760\times 2=1.520& \text{ parte intera 1}\\ 0.520\times 2=1.040& \text{ parte intera 1}\\ 0.040\times 2=0.080& \text{ parte intera 0}\\ ...& \end{array}$$

quindi il numero $0.215_{10}$ in base 2 diventa $\mathrm{0.001101110..}{.}_2$.

Conversione di un qualsiasi numero reale

1. Determinare il segno di $\alpha$
2. Determinare la parte intera $\lfloor |\alpha |\rfloor$ eseguendo la conversione con l’algoritmo delle divisioni successive
3. Determinare la parte frazionaria $|\alpha |-\lfloor |\alpha |\rfloor$ eseguendo la conversione con l’algoritmo delle moltiplicazioni successive
4. La conversione finale è segno, conversione parte intera, punto radice e conversione parte frazionaria